El racionamiento o inferencia

El Racionamiento o inferencia

El razonamiento o inferencia

Hasta aquí hemos considerado las proposiciones y sus conexiones. Ahora vamos a observar la relación interna de las proposiciones y el modo de progresar en el conocimiento, obteniendo conclusiones a partir de proposiciones ya conocidas. Es el razonamiento o inferencia.

Razonar es un proceso progresivo de la mente, que va de unas proposiciones ya conocidas llamadas premisas a otra nueva llamada conclusión. La conclusión está en parte contenida en las premisas, de modo que para que el razonamiento esté bien construido tiene que haber una relación de necesidad entre las premisas y la conclusión. La conclusión se deriva necesariamente de las premisas. Por ejemplo, cuando descargo un camión de muebles, extraigo éstos del interior, y es en ese momento cuando puedo apreciarlos en su conjunto. Sacar conclusiones es derivarlas de las proposiciones anteriores o premisas:

"Si estudio, aprendo. Es así que estudio, luego aprendo".

La conclusión de un razonamiento es la proposición que se afirma sobre la base de las otras proposiciones que nos dan los elementos de juicio o razones para aceptar la conclusión.

En el lenguaje formal la conclusión va precedida del símbolo  que se lee "luego".

El razonamiento anterior se simboliza:

1.		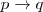( primera premisa )
2.		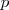( segunda premisa )
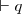		(conclusión)

Un razonamiento bien construido puede ser falso en su contenido material, por ejemplo si digo:

"Todos los burros vuelan".

"Platero es un burro".

Luego "Platero vuela".

El razonamiento es materialmente falso pero es válido lógicamente porque está bien construido. A la lógica sólo le importa la validez formal.

Otro ejemplo descabellado puede ser:

"La tierra está formada de plastilina".

"Mi brazo forma parte de la tierra".

Luego "Mi brazo está formado de plastilina".

El razonamiento es lógica o formalmente verdadero porque la lógica busca que la conclusión se derive necesariamente de las premisas, y no una verdad de hecho.

Puede darse el caso, sin embargo, de razonamientos que sean verdaderos materialmente y válidos formalmente, por ejemplo:

"Quien no se presente a examen, suspenderá".

"Pepa no se ha presentado".

Luego "Pepa suspende". 

En resumen, en lógica no interesa tanto la verdad o falsedad de las proposiciones, sino las relaciones lógicas que existen entre ellas.

Un razonamiento es válido cuando la conclusión se deriva necesariamente de las premisas y es inválido cuando la conclusión no se deriva de las premisas.

Ejemplos de razonamiento:

Ejercicicos Propuestos

Ejercicios Resueltos

Simboliza las siguientes expresiones

1. Las computadoras trabajan más rápido que los hombres.
2. No tengo un auto azul.
3. Marcela estudia en Quito y Pablo en Loja.
4. Bailamos o tomamaos café.
5. Si cantamos entonce necesitamos viajar.
6. Leere este libro si solo si tiene pocas hojas.
7. No es cierto que si no tomamos café implica que no es de día.
8. La tierra gira alrededor del sol ó no se da que la luna es un planeta.
9. Si trabajara los fines de semana y durmiera menos entonces no perdería el vuelo.
10. Es falso que vivo en Loja, pero visitaré a mi familia en Cuenca.
11. No iremos al partido a menos que salga el sol.
12. Ana es profesora o es estudiante pero no puede ser ambas cosas a la vez.

Construcción de tablas de verdad

CONSTRUCCION DE TABLAS DE VERDAD

En la construcción de tablas de verdad debemos tener los siguientes hechos:

1. Determinar el número posibles de combinaciones. Si hay  proposiciones, el número de combinaciones será

2. Se debe procurar respetar el orden de los valores de verdad dentro de la tabla así por ejemplo:

Si hay tres proposiciones, el número de combinaciones serán ; por lo tanto para primera proposición  serán 4 verdaderas y 2 falsas; para la segunda proposición 2 verdaderas y 2 falsas; para la tercera: una verdadera y la otra falsa.

3. Si la última casilla o columna son todas verdaderas, se dice que la proposición es una tautología.

Ejemplos:

1. Construir la tabla de verdad para:                                          
2. Construir la tabla de verdad para:                                                                                                                               
3. Construir la tabla de verdad para :